毎週木曜日は定例活動日です。
今日はアルゴリズム入門ということで、頻出する「累積和」とその応用、「いもす法」について勉強しました。


累積和とは?
累積和とは、「配列のある範囲の和を高速に求めるアルゴリズム」です。
例えば、以下のような大きさNの配列を考えてみましょう。
A[] = {3, 1, 4, 1, 5, 9, 2, 6, …}
この、A[2] から A[5] までの和を求めたいとします。
普通に考えると、for文などでA[2]からA[5]まで足し上げる以下のような実装が浮かぶと思います。
int sum = 0;
for(int i=2; i<=5; i++){
sum += A[i];
}
愚直な実装ですが、これを何度も繰り返すとなるとどうでしょう?
M回繰り返すとして、計算量は\(O(MN)\) になります。
何度も同じ足し算をやることになる気がするので、もう少し高速化できそうです。
そこで、すべての要素を足し上げた配列 sum_A[] を考えます。
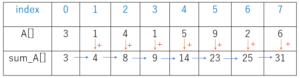
このような配列を考えると、任意の範囲の和を1回の計算で求めることが可能です。
例えば、A[2]からA[5]までの和を求めたい場合は、A[5] - A[1]とすることで求められます。
一般に、A[i]からA[j]までの和を求めたい場合は、A[j] - A[i-1]で求まります。
なぜこれで求まるの?
sum_A[i]という配列は、「0からiまでの要素の和」を格納しています。
ということは、この計算は「0からiまでの要素の和」から「0からj-1までの要素の和」を引いている事になり、つまりは「jからiまでの要素の和」になるのです。
M回繰り返すとして、計算量は\(O(N+M)\)になります (sum_A[]の計算に\(O(N)\)かかります)。
いもす法とは?
いもす法は累積和を応用したテクニックです。
いもす法は、「範囲のリストが与えられたとき、ある要素がいくつ範囲内に収まっているか」を高速に求めるアルゴリズムです。
若干わかりにくいので、例を。
あるお店の1日の営業N秒間(\(0 \leq t \leq 10^7\))について、客M人がそれぞれ何時から何時までいたのかをリスト化したものがあるとしましょう。
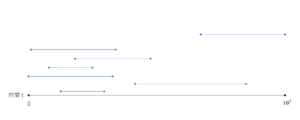
こんな感じです。あなたの仕事は、一番客が多かった時間がいつなのかを求めることです。
愚直な解法を考えると、時間の配列 t [N]を持っておいて、各範囲を満たす値について+1していく、というものです。
#include<iostream>
#include<string.h>
int t[10000001];
int main(){
memset(t, 0, sizeof(t));
for(int i=0; i<M; i++){
int l,r;
cin >> l >> r;
for(int j=l; j<=r; j++){
t[j]++;
}
}
// …
}
memset(配列, 値, sizeof(配列));は配列を特定の値(基本0か-1のみ)で初期化するものです。string.hのincludeが必要です。
この関数は、1バイトごとに指定された値で埋めていくので、値に1(16進数: 0x01)を指定すると、int型配列の場合各要素が0x01010101 で埋められることになってしまいます(int型は4バイト)。なので基本0か-1でのみ埋められると覚えておくと良いでしょう。
さて、これでは範囲が非常に大きい場合、足していく操作で非常に時間がかかってしまいます。計算量にすると、\(O(MN)\)です。
累積和をどう応用する?
ここで累積和の応用、「いもす法」の出番です。
この問題の肝は、「入った時間と出た時間さえわかれば良い」ということです。
入店した時間に+1、退店した直後の時間に-1を記録していきます。
これで、累積和でやったような計算を行うと、店にいた時間が復元されます。
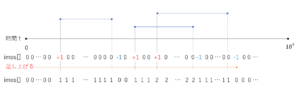
複数重なっていても大丈夫です。こうすることで、計算量は\(O(M+N)\)になります。
コードに起こしてみましょう。
#include<iostream>
int imos[10000001];
int main(){
int N,M;
cin >> N >> M;
memset(imos, 0, sizeof(imos));
for(int i=0; i<M; i++){
int l,r;
cin >> l >> r;
imos[l]++;
imos[r+1]--;
}
for(int i=0; i<N-1; i++){
imos[i+1] += imos[i]; // 累積和の計算
}
// …
}
演習
さて、累積和といもす法を使う問題をいくつか紹介しておきます。
Codeforces 816B 「Karen and Coffee」
いずれも累積和といもす法で解けます。
「オセロ」の問題と、解法も紹介しておきます。
N個の黒を向いたオセロコマが並んでおり、l個目からr個目までのコマを裏返す操作をQ回行います。このとき、コマの並びを出力する、というものです。
裏返した回数をimos[]に記録し、その偶奇で0と1を表示させればOKです。
コード例です。
#include<iostream>
#include<string.h>
using namespace std;
int imos[200001];
int main(){
int N, Q;
cin >> N >> Q;
memset(imos, 0, sizeof(imos));
for(int i=0; i<Q; i++){
int l,r;
cin >> l >> r;
l--; r--; // 0-originにする
imos[l]++;
imos[r+1]--;
}
cout << imos[0]%2;
for(int i=0; i<N-1; i++){
imos[i+1] += imos[i];
cout << imos[i+1]%2;
}
cout << "\n";
return 0;
}
そろそろ文化祭でみんなも忙しそう。私も他のサークルのコーディングで死にそうです。
writer: サー長
Pingback: 10/26定例勉強会「第一回バーチャルコンテスト」 | 東北大学puzzleknot 公式サイト